How long does a salt battery last?
The life of a battery of any type depends on various parameters, such as temperature (lead, lithium), depth of discharge (all batteries), charging and discharging currents (all batteries), length of storage before use (lithium, lead), etc.
An important parameter is the charging and discharging power (current intensity of charging and discharging). If a battery is very heavily loaded, such as in an e-vehicle, then the battery will not live as long as if it is only rarely discharged, as is the case with a UPS system.
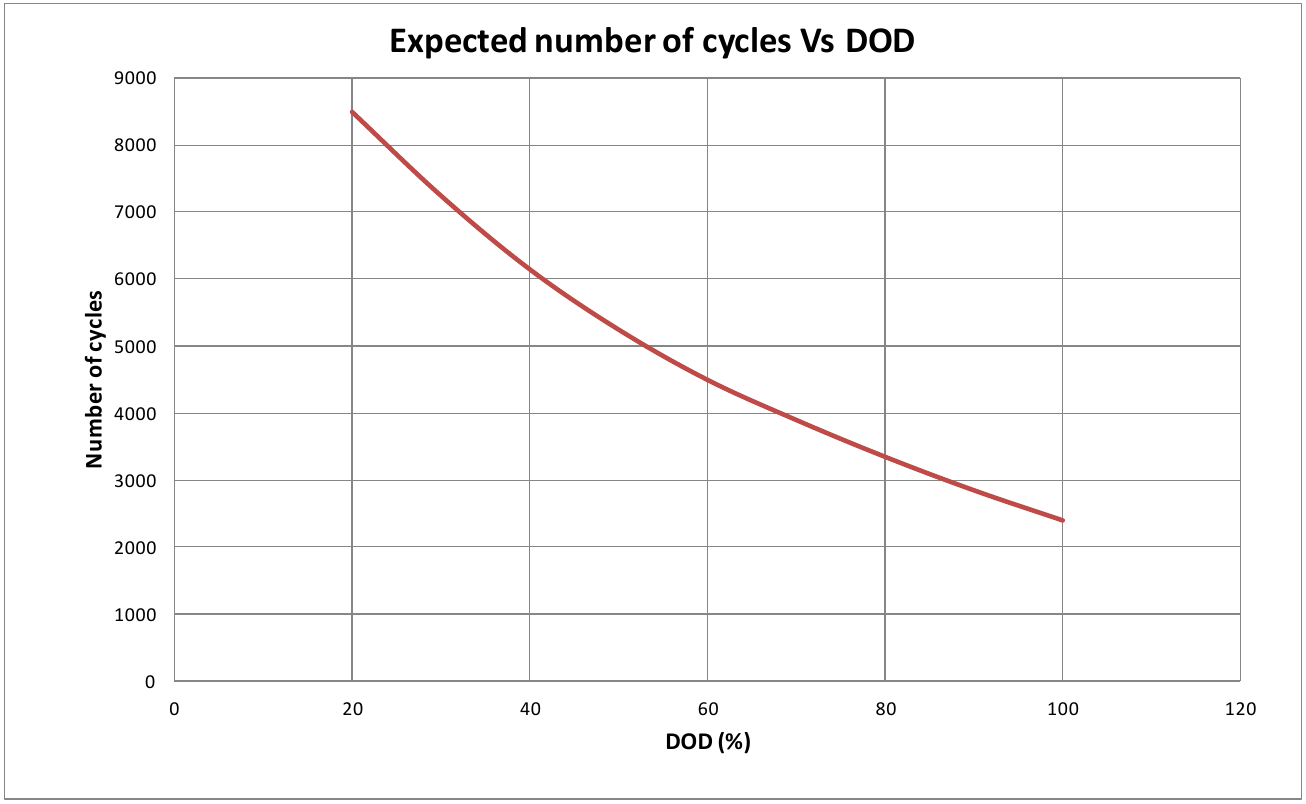
The cycle depth also plays a role. For the salt battery, this can be seen in the following diagram. It should be noted that this curve is a "synthetic" curve derived from accelerated cell tests in the laboratory. After all, you can't wait 20 years for the tests to be completed. The diagram shows a life expectancy, i.e. an average life span for a standard cycle.
State of charge, calibration and deep discharge of a salt battery
A salt battery is operated between 20% and 100% SOC (State of Chage). Every seven days, the battery should be charged to 100% so that the SOC is calibrated again. If the battery is rarely fully charged (e.g. only once every month), the internal resistance of the battery increases and a full charge takes longer and longer. To prevent this from happening and to ensure that the battery management system (BMS) of the salt battery is calibrated, a full charge is programmed for every seven days.
A deep discharge to 0% SOC, on the other hand, has no effect on the battery capacity, according to the battery manufacturer. A unique feature of the NaNiCl battery is that it can be "switched off". This means that the salt battery is deep discharged and the internal temperature of 265 degrees cools down to ambient temperature. We call this "hibernation". This is used when the photovoltaic output drops sharply in winter and it no longer makes sense to operate a battery storage system because there is too little surplus energy.
What is the charging behaviour of a salt battery?
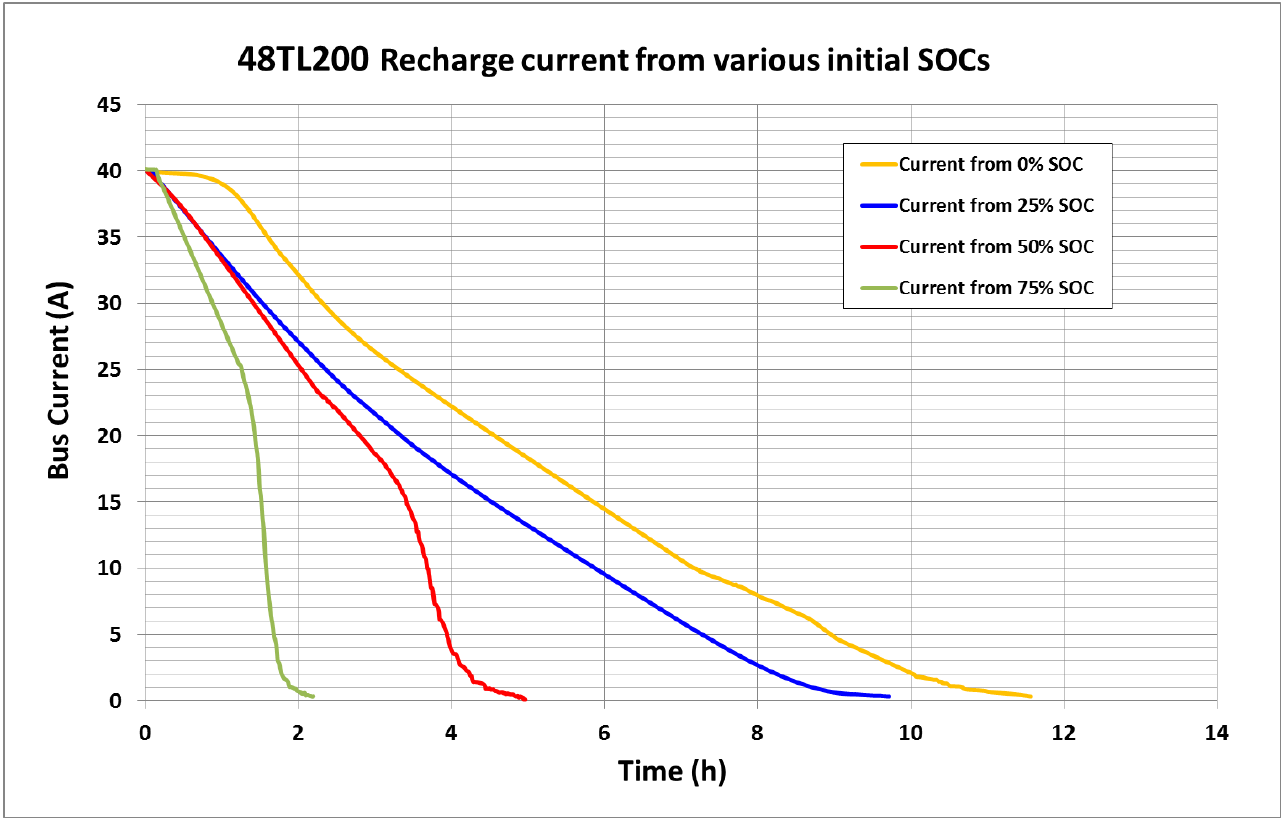
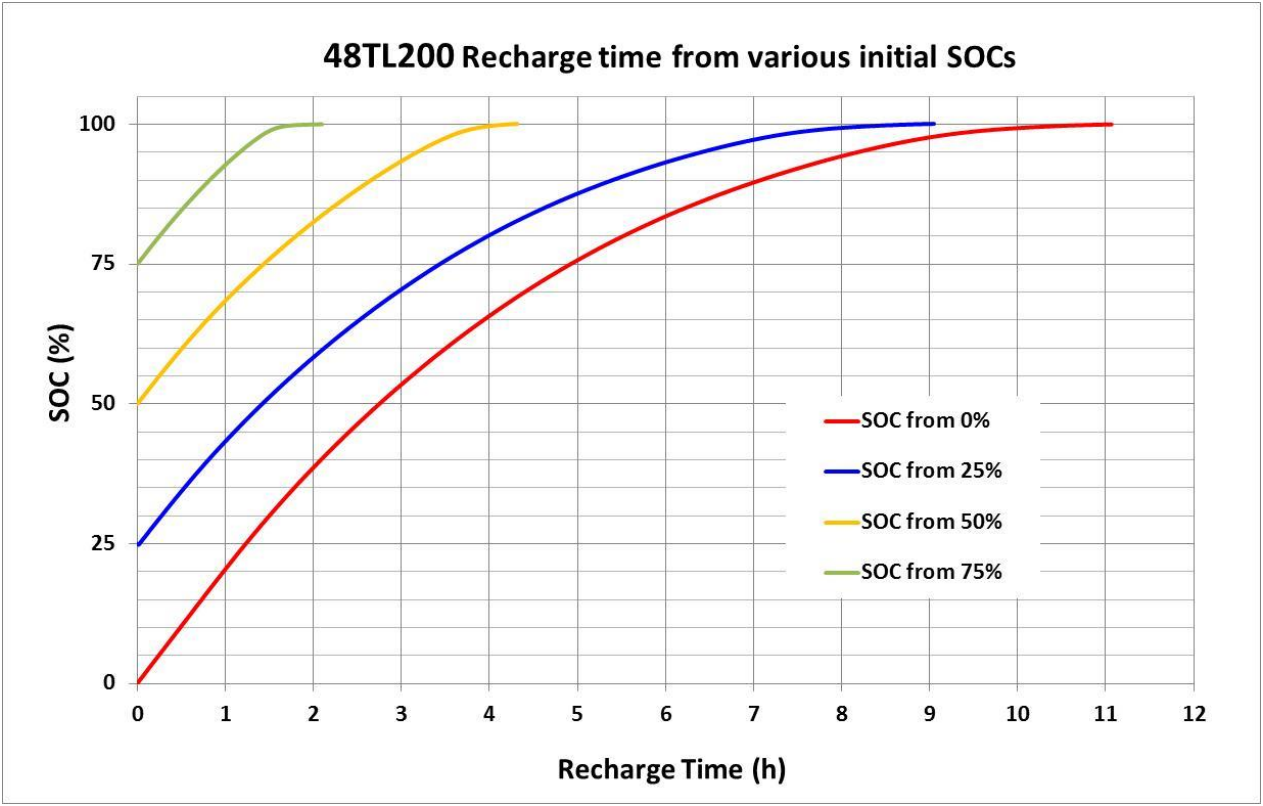
The salt-nickel battery is a "cosy" battery. It charges slowly. The battery itself - without taking the battery inverter power into account - can absorb about 2 kW of power at maximum and only for a short time (1 hour) when the battery is almost empty. The salt battery is therefore not suitable for absorbing large and short-term PV production peaks.
If larger PV production peaks are to be utilised in order to reduce the return delivery to the electricity grid, a combination of battery and thermal storage is recommended. The battery storage then takes over the basic supply of the house with its own electricity and the thermal storage (heating rod or heat pump) stores additional surplus in the form of hot water.
How long does it take to fully charge a salt battery?
What is the discharge behaviour of a salt battery?
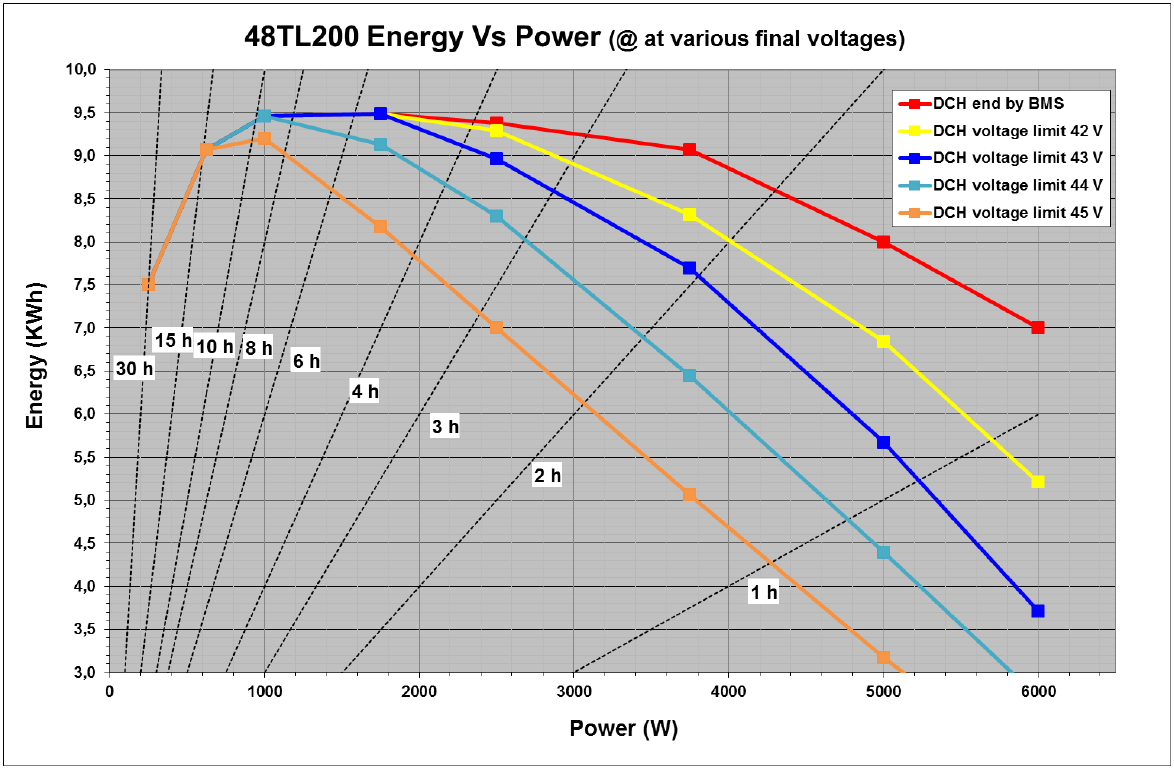
Typically, a salt battery can be discharged faster than it can be charged. A 9 kWh salt storage can be discharged with a maximum of 6 kVA continuous power.
Due to the internal resistance of the battery, the internal temperature of the salt battery increases with large discharge currents. The battery can be operated with an internal temperature between 265° Celsius and 350° Celsius. This means that this battery has the widest operating temperature range of all known batteries.
The diagram shows the energy content of the battery at different discharge rates.
How much energy is needed to bring a 9 kWh salt battery to operating temperature (250° C)?
To bring a 9 kWh salt battery to operating temperature requires 9 kWh and takes about 6-8, maximum 12 hours. If the salt battery is heated up via normal mains electricity, the costs are only about 2 CHF in Switzerland – in Germany it costs about 3 EUR. Of course, the battery can also be heated up via your own photovoltaic system.
How much power is needed to keep the 9 kWh salt battery at operating temperature?
When the salt battery is used regularly, heat is generated by the internal resistance during charging and discharging, which is used to maintain the temperature of the salt battery. When the salt battery is not used much, up to 120 watts can be consumed from the battery for temperature maintenance at peak times, depending on the degree of use. If the salt battery is not used for a longer period of time – for example in winter when there is snow on the solar panels – the salt battery can be switched off and sent into hibernation. Thus, it has no self-consumption.
With what maximum power can the batteries be discharged?
Each type of battery heats up during discharge because a battery has an "internal resistance". The internal resistance of the salt battery is greater than that of a lithium-ion battery (LIB). Thus, the salt battery heats up faster than a LIB. To prevent the saline battery from overheating during rapid discharging (internal temperature > 330° Celsius), innovenergy has limited this discharging power to 100 A per battery, which corresponds approximately to a discharging power of 5 kW.
The salidomo© ECO is a single-phase system with a single battery inverter with a capacity of 2.4 kW (or 3 kVA). The inverter can draw 2.4 kW of power from the battery.
The salidomo© 9 is a three-phase system with a rated power of 7.2 kW (or 9 kVA). The three battery inverters could draw about 7 kW from a single saline battery. However, due to the battery, only a maximum of 5 kW can be extracted. With the salidomo© 18, on the other hand, the entire inverter power of 7.2 kW can be taken from the two salt batteries.
The salidomo© EXT 27/36 is also a three-phase system with a nominal battery inverter power of 12 kW (or 15 kVA). The three batteries of the salidomo© EXT 27 can deliver a maximum of 15 kW; the four batteries of the salidomo© EXT 36 the whole 20 kW. The three battery inverters, however, can extract a maximum of 12 kW of power from the salidomo© batteries.
This discharge power applies at an operating temperature of 25° Celsius. If the temperature rises, the inverter power drops – this is called "derating".
See also technical data sheet of the inverters:
- Victron Multiplus-II/3 kVA for salidomo© 9/18
- Victron Multiplus-II/5 kVA for salidomo© EXT 27/36
What is the end-to-end efficiency of a salt battery storage system?
The standard cycle of a salt battery has been precisely defined by the manufacturer and is 90% efficiency. Any deviation from this standard cycle means a poorer efficiency. However, this also applies to all specifications of other battery manufacturers.
The final efficiency depends very much on the actual operation (charging and discharging) of the battery. If the battery size is correctly dimensioned, one can assume an average efficiency (current in, current out including inverter losses) of 60 - 65 %.
Difference PV inverter and battery inverter?
First of all, a distinction must be made between PV inverters and battery inverters. All salidomo© are AC-coupled systems, i.e. PV inverters (conversion of DC current from the PV system to AC current into the house grid) and battery inverters (conversion of AC current from the house grid to DC current into the battery) are needed.
Since all consumers in the house require AC (alternating current), charging the battery directly from the PV system only works to a limited extent. After all, the consumers are to be supplied before the battery and only the surplus electricity is to be fed into the battery. Furthermore, the PV current has a different voltage than the battery, which is operated at 48 V. The battery is then charged directly from the PV system. The AC coupling compensates for this DC voltage difference.
Does the salidomo© also work with other battery inverters?
Since the salidomo© is an AC-coupled complete system and battery inverters from Victron are already installed, it works with all PV inverters.
The salidomo© must not be operated with other battery inverters, otherwise the device certification becomes invalid and a special approval becomes legally necessary. This is a matter of liability claims, which the converter must then bear in full. innovenergy as well as the manufacturers of the components no longer provide any warranty guarantees or support in the event of a conversion.
What is the difference between an AC-coupled and a DC-coupled battery storage system?
An AC-coupled battery storage system takes the alternating current from the (domestic) grid and converts it into direct current for charging the batteries. When the batteries are discharged, the battery direct current is converted back into alternating current for the (home) grid. When converting mains current into battery current and back again, losses occur in the battery inverter. Typically, between 10% and 15% of the energy is lost as waste heat in the inverters.
Advantage: An AC-coupled battery storage system can also be installed after the PV system has been built. Disadvantage: In total, up to 20% of the PV energy is lost, because in addition to the loss of the battery inverters described above, there are also the losses of the PV inverter. The PV inverter converts the direct current from the PV modules into alternating current, which is then used to charge and discharge the batteries via the battery inverters. Here, too, losses of a few percent occur between the PV modules and the AC grid.
A DC-coupled battery storage system avoids these conversion losses and converts the direct current of the PV modules directly into direct current for charging the batteries. When discharging the batteries, the battery direct current is converted into alternating current for the grid as before.
Advantage: Lower conversion losses and seamless operation of the PV system even without an AC grid. Disadvantage: Is usually only possible with a new PV system.
The salidomo© can be operated as an AC-coupled battery storage system, as a DC-coupled battery storage system or even a combination thereof.
Which products can be used to charge the salt batteries via DC?
All Victron solar charge controllers can easily charge innovenergy's salt battery storage systems. The charging power is limited to 6 kW for the salidomo© and to 12 kW for the salidomo© EXT.
Are there any questions left unanswered?
Then simply register for one of our next info webinars or ask one of our sales partners in your area.

Info-Webinar "Store with salt!"
Learn all about salt battery storage systems in a live webinar.
Here we are also available to answer your direct questions.

Consulting & Sales
You would like personal advice, tailored to your needs for a storage solution.
A partner near you will take care of you expertly.